Linear Algebra - Vectors

import numpy as np

What is a vector?

---

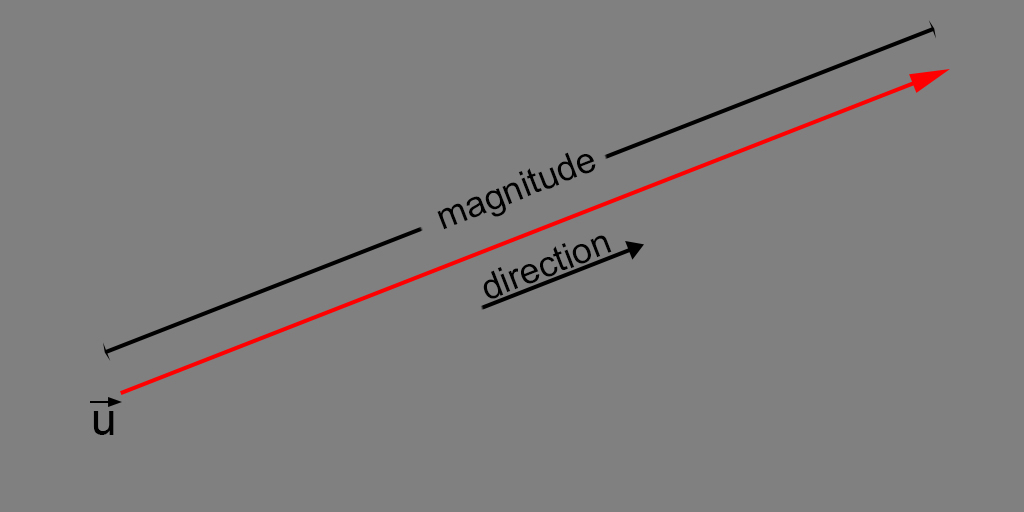
A vector \(\large \vec{v}\) is a mathematical entity which has magnitude and direction.

Vector operations

---

All the following operations are applicable to any vector in \(\large \mathbb{R}^n\).

Vector addition

---

The addition of two vectors \(\large \vec{u}\) and \(\large \vec{v}\) is done by the sum of their correspondent components, resulting in another vector.

\[\begin{split} \large \vec{u}+\vec{v} = \begin{bmatrix} u_1 \\ u_2 \\ \vdots \\ u_n \end{bmatrix} + \begin{bmatrix} v_1 \\ v_2 \\ \vdots \\ v_n \end{bmatrix} = \begin{bmatrix} v_1 + u_1 \\ v_2 + u_2 \\ \vdots \\ v_n + u_n \end{bmatrix} \end{split}\]

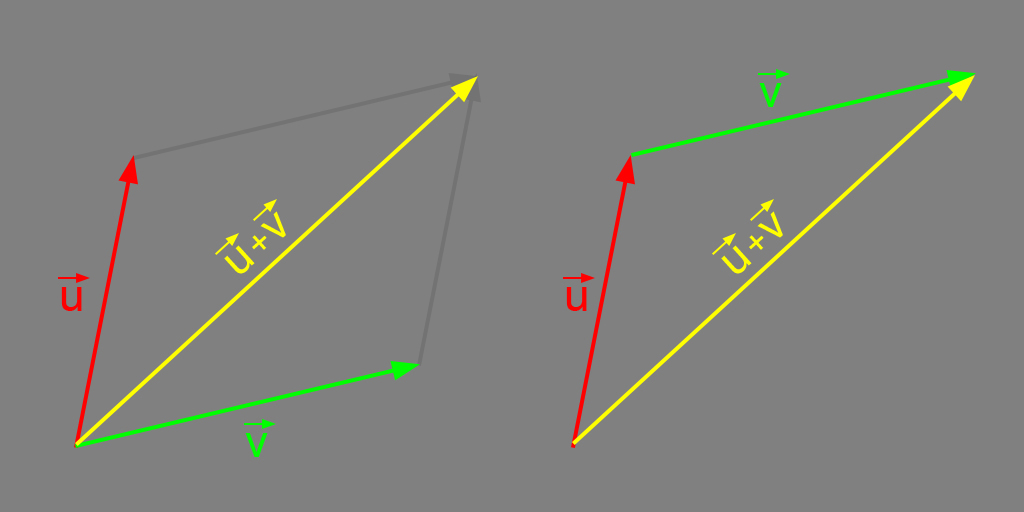
For example:

\[\begin{split} \large \vec{u} = \begin{bmatrix} 3 \\ 7 \end{bmatrix} \quad , \quad \vec{v} = \begin{bmatrix} 2 \\ 5 \end{bmatrix} \end{split}\]

\[\begin{split} \large \vec{u} + \vec{v} = \begin{bmatrix} 3 + 2 \\ 7 + 5 \end{bmatrix} = \begin{bmatrix} 5 \\ 12 \end{bmatrix} \end{split}\]

u = np.array([[3, 7]])
v = np.array([[2, 5]])
print(u.T, end=" = u\n\n")
print(v.T, end=" = v\n\n")
print((u + v).T, end=" = u + v")

Vector subtraction

---

Similarly to addition, the subtraction of two vectors \(\large \vec{u}\) and \(\large \vec{v}\) is done by the subtraction of their correspondent components, resulting in another vector.

\[\begin{split} \large \vec{u}-\vec{v} = \begin{bmatrix} u_1 \\ u_2 \\ \vdots \\ u_n \end{bmatrix} - \begin{bmatrix} v_1 \\ v_2 \\ \vdots \\ v_n \end{bmatrix} = \begin{bmatrix} v_1 - u_1 \\ v_2 - u_2 \\ \vdots \\ v_n - u_n \end{bmatrix} \end{split}\]

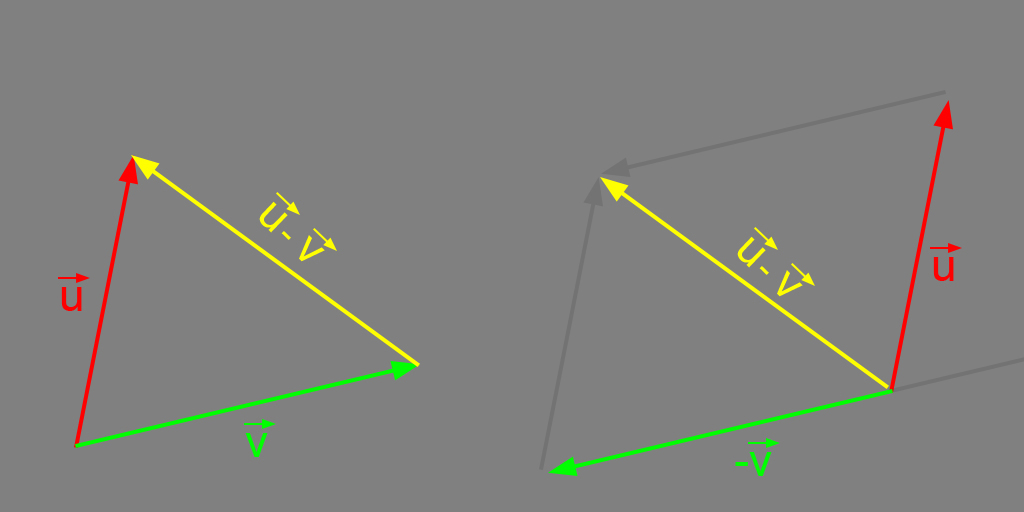
For example:

\[\begin{split} \large \vec{u} = \begin{bmatrix} 3 \\ 7 \end{bmatrix} \quad , \quad \vec{v} = \begin{bmatrix} 2 \\ 5 \end{bmatrix} \end{split}\]

\[\begin{split} \large \vec{u} - \vec{v} = \begin{bmatrix} 3 - 2 \\ 7 - 5 \end{bmatrix} = \begin{bmatrix} 1 \\ 2 \end{bmatrix} \end{split}\]

u = np.array([[3, 7]])
v = np.array([[2, 5]])
print(u.T, end=" = u\n\n")
print(v.T, end=" = v\n\n")
print((u - v).T, end=" = u - v")

Scalar multiplication

---

The scalar multiplication is the elementwise multiplication by a scalar number \(\large \alpha\). The same rule can be applied to divisions.

\[\begin{split} \large \alpha\vec{u} = \alpha \cdot \begin{bmatrix} u_1 \\ u_2 \\ \vdots \\ u_n \end{bmatrix} = \begin{bmatrix} \alpha\cdot u_1 \\ \alpha\cdot u_2 \\ \vdots \\ \alpha\cdot u_n \end{bmatrix} \end{split}\]

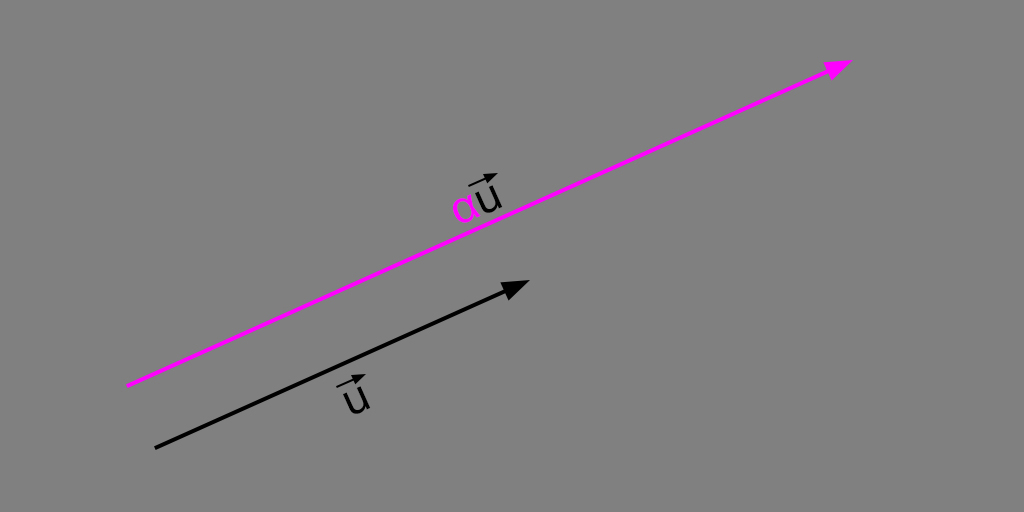
For example:

\[\begin{split} \large \alpha = 2 \quad , \quad \vec{u} = \begin{bmatrix} 3 \\ 7 \end{bmatrix} \end{split}\]

\[\begin{split} \large \alpha\cdot\vec{u} = \begin{bmatrix} 2 \cdot 3 \\ 2 \cdot 7 \end{bmatrix} = \begin{bmatrix} 6 \\ 14 \end{bmatrix} \end{split}\]

a = 2
u = np.array([[3, 7]])
print(a, end=" = a\n\n")
print(u.T, end=" = u\n\n")
print(a*u.T, end=" = au")

Dot product

---

Dot product is an algebraic operation, which has a huge number of applications. As a result, we have a scalar value.

\[\begin{split} \large \vec{u} \cdot \vec{v} = \begin{bmatrix} u_1 \\ u_2 \\ \vdots \\ u_n \end{bmatrix} \cdot \begin{bmatrix} v_1 \\ v_2 \\ \vdots \\ v_n \end{bmatrix} = \sum_i^n u_i \cdot v_i \end{split}\]

\[ \large \sum_i^n u_i \cdot v_i = u_1 \cdot v_1 + u_2 \cdot v_2 + ... + u_n \cdot v_n \]

For example:

\[\begin{split} \large \vec{u} = \begin{bmatrix} 3 \\ 7 \end{bmatrix} \quad , \quad \vec{v} = \begin{bmatrix} 2 \\ 5 \end{bmatrix} \end{split}\]

\[\begin{split} \large \begin{aligned} \vec{u} \cdot \vec{v} &= 3 \cdot 2 + 7 \cdot 5 \\ &= 6 + 35 \\ &= 41 \end{aligned} \end{split}\]

u = np.array([3, 7])
v = np.array([2, 5])
print(u, end=" = u\n\n")
print(v, end=" = v\n\n")
print(np.dot(u, v), end=" = u.v")

Unit vector

---

Unit vector (or versor) is a vector which has the magnitude equal to 1. The magnitude of a vector is based on the euclidean norm and can be found by:

\[ \large \|\vec{u}\|_2 = \left[ \sum_i^n u_i^2 \right]^{\frac{1}{2}}=\sqrt{u_1^2+u_2^2+...+u_n^2} \]

Basically, a unit vector is a normalized vector, like:

\[ \large \hat{u}=\frac{\vec{u}}{\|\vec{u}\|} \]

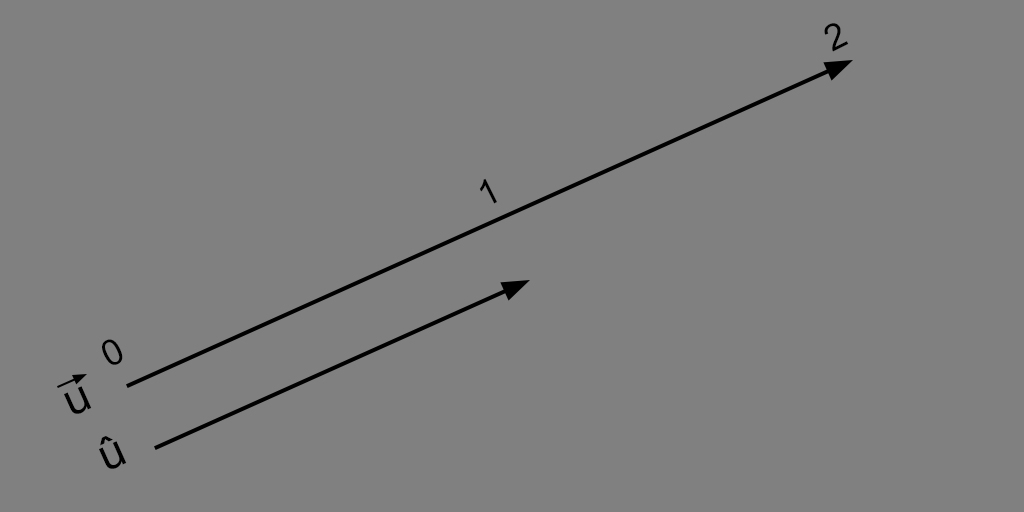
For example:

\[ \large \vec{u} = [3 \quad 4] \]

\[\begin{split} \large \begin{aligned} \|\vec{u}\| &= \sqrt{3^2+4^2} \\ &= \sqrt{9+16} \\ &= 5 \end{aligned} \end{split}\]

\[ \large \frac{\vec{u}}{\|\vec{u}\|} = \left[ \frac{3}{5} \quad \frac{4}{5} \right] = [0.6 \quad 0.8] \]

u = np.array([3, 4])
u_ = np.sum(u**2)**0.5
print(u, end=" = u\n\n")
print(u_, end=" = ||u||\n\n")
print(u/u_, end=" = û")

Angle between vectors

---

Given the geometric definition of dot product:

\[ \large \vec{u} \cdot \vec{v} = \|\vec{u}\| \|\vec{v}\| \cos{\theta} \]

so,

\[ \large \theta=\cos^{-1} \frac{\vec{u} \cdot \vec{v}}{\|\vec{u}\| \|\vec{v}\|} \]

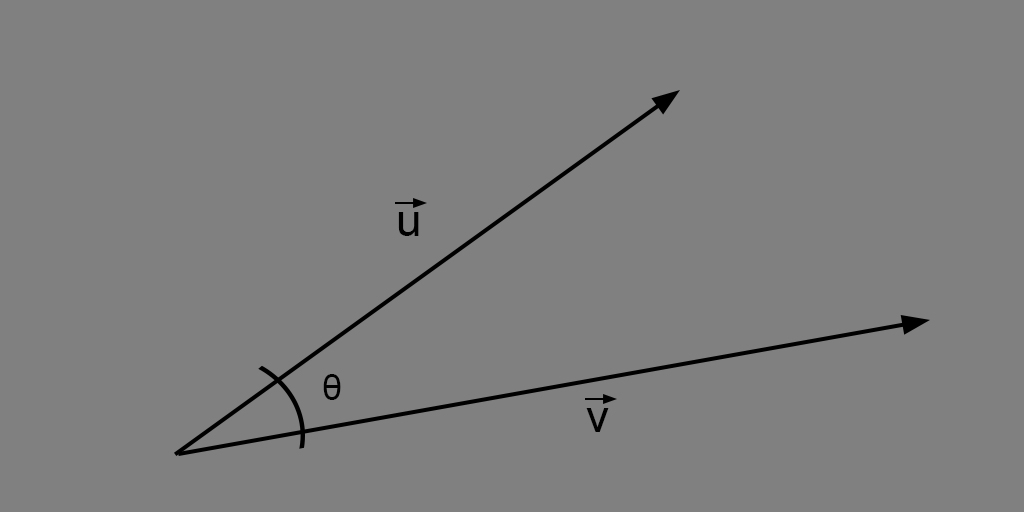
For example:

\[\begin{split} \large \vec{u} = \begin{bmatrix} 2 \\ 1 \end{bmatrix} \quad , \quad \vec{v} = \begin{bmatrix} 3 \\ 3 \end{bmatrix} \end{split}\]

\[\begin{split} \large \begin{aligned} \angle (\vec{u}, \vec{v}) = \theta &= \arccos \frac{2 \cdot 3 + 1 \cdot 3}{\sqrt{2^2+1^2} \sqrt{3^2+3^2}} \\ &= \arccos \frac{9}{\sqrt{5} \sqrt{18}} \\ &\approx 0.32 \text{rad} \quad \approx 18.43° \end{aligned} \end{split}\]

u = np.array([2, 1])
v = np.array([3, 3])
uv = np.dot(u, v)
u_ = np.sum(u**2)**0.5
v_ = np.sum(v**2)**0.5
rad = np.arccos(uv/(u_*v_))
print(u, end=" = u\n\n")
print(v, end=" = v\n\n")
print(f'{np.rad2deg(rad):.02f}', end=" = θ")

Orthogonality and Parallelism

---

Two vectors are parallel or \(\large \vec{u} // \vec{v}\) when there is a number \(k\) which generalizes the relationship:

\[ \large \vec{u} = k\vec{v} \]

What it means that:

\[ \large \frac{u_1}{v_1} = \frac{u_2}{v_2} = ... = \frac{u_n}{v_n} = k \]

In other words, two vectors are parallel when their components are proportional.

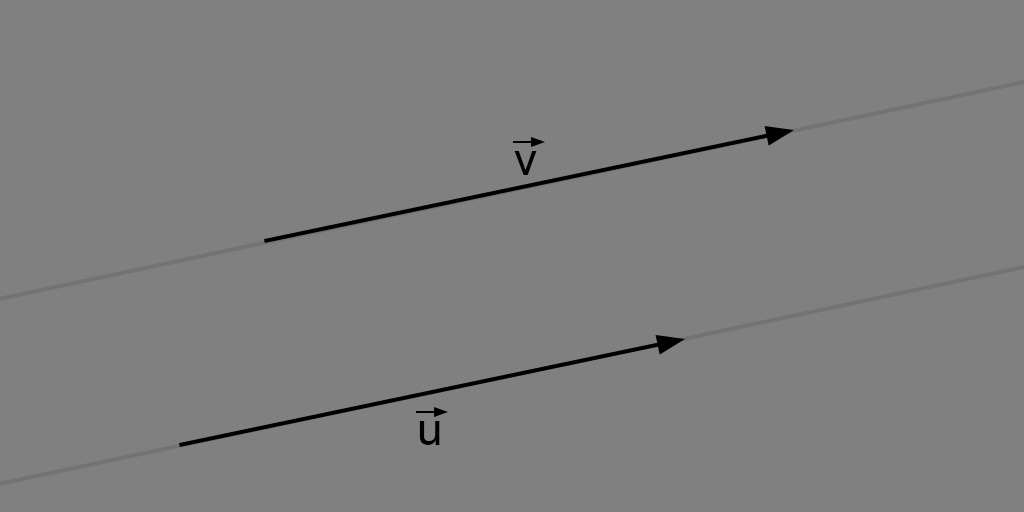
For example:

\[\begin{split} \large \vec{u} = \begin{bmatrix} 2 \\ 3 \end{bmatrix} \quad , \quad \vec{v} = \begin{bmatrix} 6 \\ 9 \end{bmatrix} \end{split}\]

\[ \large \frac{2}{6} = \frac{3}{9} = \frac{1}{3} \]

u = np.array([2, 3])
v = np.array([6, 9])
print(u, end=" = u\n\n")
print(v, end=" = v\n\n")
print(f'{u/v}', end=" = k")

Two vectors are orthogonal or \(\large \vec{u} \bot \vec{v}\) when the angle \(\theta\) between of them are 90° or their dot product is equal to 0.

\[ \large \vec{u} \bot \vec{v} \Rightarrow \vec{u} \cdot \vec{v} = 0 \]

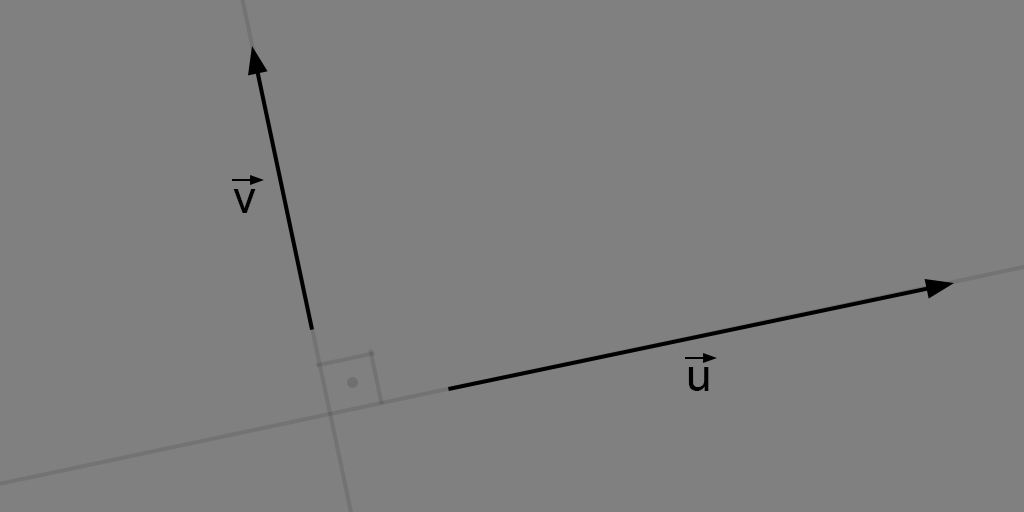
For example:

\[\begin{split} \large \vec{u} = \begin{bmatrix} 2 \\ 1 \end{bmatrix} \quad , \quad \vec{v} = \begin{bmatrix} -2 \\ 4 \end{bmatrix} \end{split}\]

We can find it by calculating the dot product:

\[ \large \vec{u} \cdot \vec{v} = 2 \cdot (-2) + 1 \cdot 4 = 0 \]

or by finding \(\theta\):

\[\begin{split} \large \begin{aligned} \angle (\vec{u}, \vec{v}) = \theta &= \arccos \frac{2 \cdot (-2) + 1 \cdot 4}{\sqrt{2^2+1^2} \sqrt{(-2)^2+4^2}} \\ &= \arccos \frac{0}{\sqrt{5} \sqrt{20}} \\ &\approx 1.57 \text{rad} \quad = 90° \end{aligned} \end{split}\]

u = np.array([2, 1])
v = np.array([-2, 4])
uv = np.dot(u, v)
u_ = np.sum(u**2)**0.5
v_ = np.sum(v**2)**0.5
rad = np.arccos(uv/(u_*v_))
print(u, end=" = u\n\n")
print(v, end=" = v\n\n")
print(uv, end=" = u.v\n\n")
print(f'{np.rad2deg(rad):.02f}', end=" = θ")